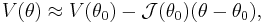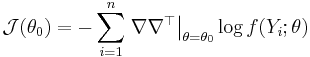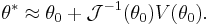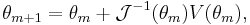Scoring algorithm
In statistics, Fisher's scoring algorithm is a form of Newton's method used to solve maximum likelihood equations numerically.
Contents |
Sketch of Derivation
Let  be random variables, independent and identically distributed with twice differentiable p.d.f.
be random variables, independent and identically distributed with twice differentiable p.d.f. 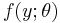 , and we wish to calculate the maximum likelihood estimator (M.L.E.)
, and we wish to calculate the maximum likelihood estimator (M.L.E.) 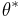 of
of  . First, suppose we have a starting point for our algorithm
. First, suppose we have a starting point for our algorithm 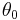 , and consider a Taylor expansion of the score function,
, and consider a Taylor expansion of the score function, 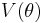 , about
, about 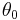 :
:
where
is the observed information matrix at 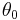 . Now, setting
. Now, setting 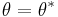 , using that
, using that 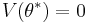 and rearranging gives us:
and rearranging gives us:
We therefore use the algorithm
and under certain regularity conditions, it can be shown that 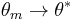 .
.
Fisher scoring
In practice, 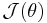 is usually replaced by
is usually replaced by ![\mathcal{I}(\theta)= \mathrm{E}[J(\theta)]](/2012-wikipedia_en_all_nopic_01_2012/I/30b6e6e51ac8819c7151b181adee57d5.png) , the Fisher information, thus giving us the Fisher Scoring Algorithm:
, the Fisher information, thus giving us the Fisher Scoring Algorithm:
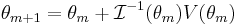 .
.